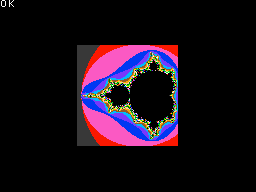
マンデルブロ集合の描画 by Dr.K
コンピューターで描く図形といえばおなじみ、マンデルブロ集合をプチコンで再現したプログラムだ。
マンデルブロ集合についてある程度理解しているとして解説すると、計算するガウス平面の実軸範囲を変数RSとSE、虚軸範囲をISとIEで定義している。これらの数値を狭めていけば、描画されるパターンが変化するのがわかるだろう。
3行目の変数KSは画面上の描画サイズ。6行目で図形を画面中央に描く調整をしている。
私が作りました
Dr.K
マンデルブロ集合を描くプログラムです。GOTO文を使ったのは何年ぶりだろう……
 CHECK POiNT
CHECK POiNT 

マンデ……ブ……?

フラ……?

ボクにもこれは難しい……。

まあピンときづらい話ではあるかのう。これこそ検索してみるのが一番かもしれん。
インテリ君の言う通り、こんなシンプルなプログラムでこんな複雑な図形が描かれる、というところが神秘的でロマンチックなところじゃ。
インテリ君の言う通り、こんなシンプルなプログラムでこんな複雑な図形が描かれる、というところが神秘的でロマンチックなところじゃ。

ロマンチックだと……?

それは違う意味でハカセの言うことが分からないってことだね。
プログラムリスト
- CLEAR:CLS:GCLS:BGMPLAY 15
- VISIBLE 1,1,0,0,0,1
- KL=100:KS=100
- RS=-2.1:RE=0.5
- IS=-1.3:IE=1.3
- BX=(255-KS)/2:BY=(191-KS)/2
- DR=(RE-RS)/KS:DI=(IE-IS)/KS
- FOR CI=IS TO IE STEP DI
- FOR CR=RS TO RE STEP DR
- ZR=0:ZI=0:K=1
- @CAL
- IF K>KL GOTO @EXIT
- R=ZR*ZR-ZI*ZI+CR
- I=2*ZR*ZI+CI
- IF (R*R+I*I)>4 GOTO @DRAW
- ZR=R:ZI=I:K=K+1:GOTO @CAL
- @DRAW
- PX=BX+(CR-RS)/DR
- PY=BY+(CI-IS)/DI
- GPSET PX, PY, K%16
- @EXIT
- NEXT CR
- NEXT CI
- BGMPLAY 6